Logical/physical operators
Logical operators
what they do
e.g., union, selection, project, join, grouping
Physical operators
how they do it
e.g., nested loop join, sort-merge join, hash join, index join
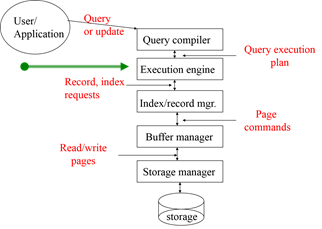
Query Execution Plans
select C.cust_name from Sale S, Manufacturer M, Customer C, Product P where M.city = 'Lima' and P.prod_id = S.prod_id and P.manufactr_id = M.manufactr_id and S.cust_id = C.cust_id
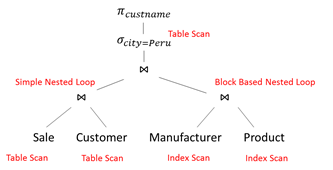
Create a Query Plan:
- logical tree
- implementation choice at every node
- scheduling of operations.
Some operators are from relational algebra, and others (e.g., scan, group) are not.
Cost Parameters
Cost parameters
- M = number of blocks that fit in main memory
- B(R) = number of blocks holding R
- T(R) = number of tuples in R
- V(R,a) = number of distinct values of the attribute a
Estimating the cost:
- Important in optimization (next lecture)
- Compute I/O cost only
- We compute the cost to read the tables
- We don’t compute the cost to write the result (because pipelining)
Sorting
Two pass multi-way merge sort
Step 1:
- Read M blocks at a time, sort, write
- Result: have runs of length M on disk
Step 2:
- Merge M-1 at a time, write to disk
- Result: have runs of length M(M-1)»M2
Cost: 3B(R), Assumption: B(R) < M2
Scanning Tables
The table is clustered (I.e. blocks consists only of records from this table):
- Table-scan: if we know where the blocks are
- Index scan: if we have index to find the blocks
The table is unclustered (e.g. its records are placed on blocks with other tables)
- May need one read for each record
Clustered relation:
- Table scan: B(R); to sort: 3B(R)
- Index scan: B(R); to sort: B(R) or 3B(R)
Unclustered relation
- T(R); to sort: T(R) + 2B(R)
One Pass Algorithms
Selection $\sigma$(R), projection $\pi$(R)
- Both are tuple-at-a-Time algorithms
- Cost B(R)

Duplicate elimination $\delta$(R)
Need to keep a dictionary in memory:
- balanced search tree
- hash table
- etc
Cost: B(R)
Assumption: B(d(R)) <= M
Grouping: $\gamma$city, sum(price) (R)
- Need to keep a dictionary in memory
- Also store the sum(price) for each city
- Cost: B(R)
- Assumption: number of cities fits in memory
Binary operations: R $\cap$ S, R $\cup$ S, R – S
- Assumption: min(B(R), B(S)) <= M
- Scan one table first, then the next, eliminate duplicates
- Cost: B(R)+B(S)
Nested Loop Joins
Tuple-based nested loop R $\bowtie$ S
R=outer relation, S=inner relation
for each tuple r in R do
for each tuple s in S do
if r and s join then output (r,s)
Cost: T(R) T(S), sometimes T(R) B(S)
Block-based Nested Loop Join
for each (M-1) blocks bs of S do
for each block br of R do
for each tuple s in bs do
for each tuple r in br do
if r and s join then output(r,s)
Cost:
• Read S once: cost B(S)
• Outer loop runs B(S)/(M-1) times, and each time need to read R: costs B(S)B(R)/(M-1)
• Total cost: B(S) + B(S)B(R)/(M-1)
Notice: it is better to iterate over the smaller relation first– i.e., S smaller
Two Pass algorithms (based on sorting)
Duplicate elimination $delta$(R)
Simple idea: like sorting, but include no duplicates
Step 1: sort runs of size M, write
- Cost: 2B(R)
Step 2: merge M-1 runs, but include each tuple only once
- Cost: B(R)
- Total cost: 3B(R), Assumption: B(R)<= M2
Index-based algorithms (zero pass)
In a clustered index all tuples with the same value of the key are clustered on as few blocks as possible:

Index based selection
Selection on equality: $\sigma_{a=v}$(R)
Clustered index on a: cost B(R)/V(R,a)
Unclustered index on a: cost T(R)/V(R,a)
Example: B(R) = 2000, T(R) = 100,000, V(R, a) = 20, compute the cost of $\sigma_{a=v}$(R)
Cost of table scan:
- If R is clustered: B(R) = 2000 I/Os
- If R is unclustered: T(R) = 100,000 I/Os
Cost of index based selection:
- If index is clustered: B(R)/V(R,a) = 100
- If index is unclustered: T(R)/V(R,a) = 5000
Notice: when V(R,a) is small, then unclustered index is useless
Index based join
R $\bowtie$ S
Assume S has an index on the join attribute
Iterate over R, for each tuple fetch corresponding tuple(s) from S
Assume R is clustered. Cost:
- If index is clustered: B(R) + T(R)B(S)/V(S,a)
- If index is unclustered: B(R) + T(R)T(S)/V(S,a)
Assume both R and S have a sorted index (B+ tree) on the join attribute
- Then perform a merge join (called zig-zag join)
Cost: B(R) + B(S)
Estimating Sizes
S = $\sigma_{a=c}(R)$
- T(S) can be anything from 0 to T(R) – V(R,A) + 1
- Mean value: T(S) = T(R)/V(R,A)
S = $\sigma_{a<c}(R)$
- T(S) can be anything from 0 to T(R)
- Heuristics: T(S) = T(R)/3
Estimating the size of a natural join, R join S
- When the set of A values are disjoint, then T(R join S) = 0
- When A is a key in S and a foreign key in R, then T(R join S) = T(R)
- When A has a unique value, the same in R and S, then T(R join S) = min(T(R), T(S))
In general: T(R join S) = T(R) T(S) / max(V(R,A),V(S,A))
- T(R) = 10000, T(S) = 20000
- V(R,A) = 100, V(S,A) = 200
- How large is R$\bowtie$S ? = 10000*20000/200 = 1000000
Query Optimization
At the heart of the database engine
- Step 1: convert the SQL query to some logical plan
- Step 2: find a better logical plan, find an associated physical plan
SQL –> Logical Query Plans:
select a1, …, an from R1, …, Rk Where C $\rightarrow$ $\pi$a1,…,an($\sigma$C(R1 x R2 x … x Rk))
Now we have one logical plan
Algebraic laws:
foundation for every optimization
Two approaches to optimizations:
- Rule-based (heuristics): apply laws that seem to result in cheaper plans
- Cost-based: estimate size and cost of intermediate results, search systematically for best plan
Optimizer has three things:
- Algebraic laws
- An optimization algorithm
- A cost estimator
Algebraic Laws
Commutative and Associative Laws
- R $\cup$ S = S $\cup$ R, R $\cup$ (S $\cup$ T) = (R $\cup$ S) $\cup$ T
- R ∩ S = S ∩ R, R ∩ (S ∩ T) = (R ∩ S) ∩ T
- R ⋈ S = S ⋈ R, R ⋈ (S ⋈ T) = (R ⋈ S) ⋈ T
Distributive Laws
- R ⋈ (S $\cup$ T) = (R ⋈ S) $\cup$ (R ⋈ T)
Laws involving selection:
- s C AND C’(R) = s C(s C’(R)) = s C(R) ∩ s C’(R)
- s C OR C’(R) = s C(R) $\cup$ s C’(R)
- s C (R ⋈ S) = s C (R) ⋈ S
When C involves only attributes of R
- s C (R – S) = s C (R) – S
- s C (R $\cup$ S) = s C (R) $\cup$ s C (S)
- s C (R ∩ S) = s C (R) ∩ S
Rule Based Optimization
Query rewriting based on algebraic laws
Result in better queries most of the time
Heuristic number 1: Push selections down
Example:
select C.cust_name from Sale S, Manufacturer M, Customer C, Product P where M.city = 'Lima' and P.prod_id = S.prod_id and P.manufactr_id = M.manufactr_id and S.cust_id = C.cust_id

Heuristics number 2: Sometimes push selections up, then down
When would this be helpful? Come up with an example, when pushing selections up and then back down would be helpful.