- [15 points] Recall that 1 block is 1 disk sector; and 1 disk sector is 4KB (4096 bytes). Let the schema of a table be:
create table midterm_grades (
netid CHAR(8) character set latin1,
q1_score INT,
q1_comments char(100) character set utf8,
q2_score INT,
q2_comments char(100) character set latin1,
q3_score INT,
q3_comments char(100) character set latin1,
q4_score INT,
q4_comments char(100) character set utf8,
extra_credit TINYINT
)
Let’s say that the average comment length is 20 characters long, and that each record header contains 12 bytes of important record information.
Answer the following questions:
a. How many bytes is does the average record consume? (show your work)
Header = 12
Netid = 8*1
[Score = 4
Comment = 20*1+1]
^^ * 2
[Score = 4
Comment = 20*3+1] //*3 for utf-8
^^ * 2
Extra credit = 1
Total = 12 + 8 + (4+20+1) * 2 + (4 + 20*3 + 1) * 2 + 1 = 201
b. About 1040 students have taken my databases midterm at Notre Dame (total). Given that records may not span more than one disk sector. How many sectors are needed to store all the midterm records?
201x$\le$4096
x = 20 tuples can fit on a single block
20y$\ge$1040
y = 52 blocks are needed to fit 1040 tuples (exactly, surprisingly; that was not intentional)
2. [15 points] Notice that Q1 did not contain any primary key. If we add a primary key to the ndid column, then we will also need to store the index on disk too. Recalculate your answer to Q1-b to take into account a primary key using a B+ Tree on the ndid column.
You can use $d$ of either 2 or 170 (or really any number in between so long as you state it clearly and show your work).
52 blocks for the original data.
1040 ints are needed in the keys of the btree or hashtable. = 1040*4 = 4160
Plus we need 1040*8 byte pointers = 8320 (for a dense index)
(4160+8320)y > 4096. y=4 leaf nodes. Plus we need a root node for the btree. = 5 index blocks
52 blocks for data + 5 blocks for index = 57 blocks total.
3. [40 points] UTF8 encoding is a variable length encoding. This means that sometimes it uses 1 byte, sometimes it uses 2, 3, or 4 bytes to represent a character. How does it know that a character is 1 or 2 or 3 or 4 bytes?
UTF-8 distinguishes this using a unary encoding. That is, if the bits of a character start with 0, then there is only 1 byte being read for this character. 0xxxxxxx represents a 1-byte character (basically the first 127 ascii characters). If the first bits of the character start with 110xxxxx, then there will be two bytes, 1110xxxx means 3 bytes, and 11110xxx means 4 bytes. See this table for example.
| Bytes | 1st byte | 2nd byte | 3rd byte | 4th byte |
|---|---|---|---|---|
| 1 | 0xxxxxxx | |||
| 2 | 110xxxxx | 10xxxxxx | ||
| 3 | 1110xxxx | 10xxxxxx | 10xxxxxx | |
| 4 | 11110xxx | 10xxxxxx | 10xxxxxx | 10xxxxxx |
Hence, the capital ‘A’, which is 65 in decimal/ASCII is represented as 01000001 encoded as ‘A’ in UTF-8.
The winky emoji: 😉 is 128,521 in decimal which is 00000001 11110110 00001001 in binary, which is encoded into UTF8 as 11110000 10011111 10011000 10001001 (with only 21 encoded bits)
“Encoding errors” happen when a file encoded in one format is decoded in another format:
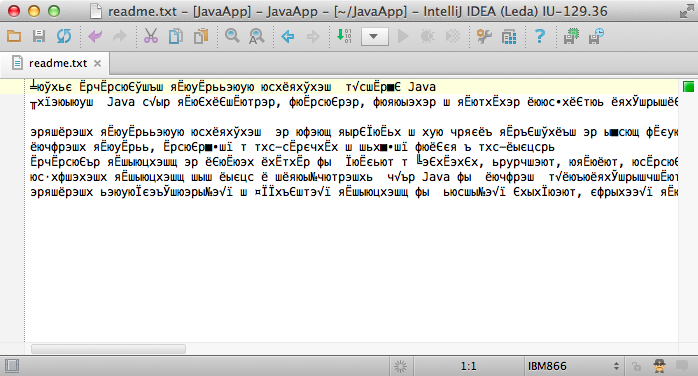
Let’s work to understand what’s happening here.
a. Let’s say that the string ‘Hi’ was encoded with ASCII.
where H is represented in decimal as 72 and
where i is represented in decimal as 105
How would it appear if decoded in UTF8?
Hi – UTF8 made ASCII as the first 127 items on purpose.
b. Let’s say that the string `选票’ (which is Chinese xuǎnpiào which translates to “vote” in English is encoded with UTF-8
where 选 is represented in decimal as 36873 and
where 票 is represented in decimal as 31080
How would it appear if decoded with ASCII (show your work)?
选票
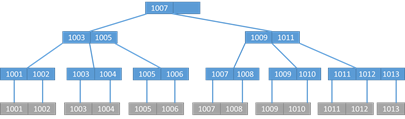
4. [25 points] Let $d$=2. Place the data from the model of the PC table below into a B+ tree indexing on the following table:
| model | speed | ram | hd | price |
|---|---|---|---|---|
| 1001 | 2.66 | 4096 | 250 | 2114 |
| 1002 | 2.10 | 2048 | 250 | 995 |
| 1003 | 1.42 | 2048 | 80 | 478 |
| 1004 | 2.80 | 4096 | 250 | 649 |
| 1005 | 3.20 | 2048 | 250 | 630 |
| 1006 | 3.20 | 4096 | 320 | 1049 |
| 1007 | 2.20 | 4096 | 200 | 510 |
| 1008 | 2.20 | 8192 | 250 | 770 |
| 1009 | 2.00 | 4096 | 250 | 650 |
| 1010 | 2.80 | 8192 | 300 | 770 |
| 1011 | 1.86 | 8192 | 160 | 959 |
| 1012 | 2.80 | 4096 | 160 | 649 |
| 1013 | 3.06 | 2048 | 80 | 529 |