Consider our textbook as an example:
How many indexes? Where?
What are keys? (keywords) What are records? (sections) What are the blocks? (page)
Clustered? (No, data is not stored in order) Dense? (Yes, there is a link to every mention of the key)
Index Limitations
Sargable (sargability?)
Remember the % opeartor?
Wildcard
Can indexes search on wildcard queries?
Yes and no
Sargable operators: =,>,<,>=,<=,BETWEEN,LIKE without leading %
Non-sargable operators <>,IN,OR,NOT IN, NOT EXISTS, NOT LIKE, LIKE with leading %
Typically non-sargable queries include a function in the left part of a where clause condition
Non sargable:
“…where phone like %7020”
How can we make this work?
B-Trees
How is this index created? What data structure is used?
B-Trees has a variant called B+ Trees (book describes a B+ tree but calls it simply B-Trees (as most people do)).
Why is it named B-Trees?
We don’t know. Balanced, bushy, broad might apply. Most likely stands for Boeing or Bayer (the guy who invented it was named Bayer and worked at Boeing)
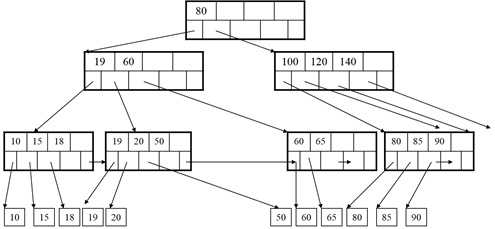
B-Tree (no +)
Idea:
Avoid duplicate keys
Have record pointers in non-leaf nodes
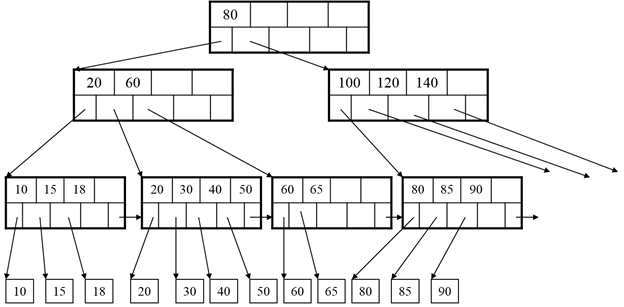
B-Tree Example:
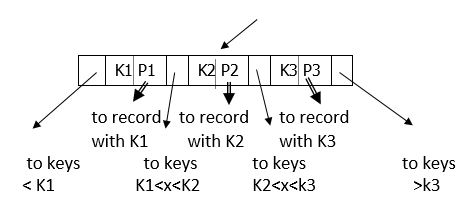
B+ Tree Basics
Parameter $d$ = the degree
Each node has [$d$, $2d$] keys (except root)
Internal node:
Leaf:
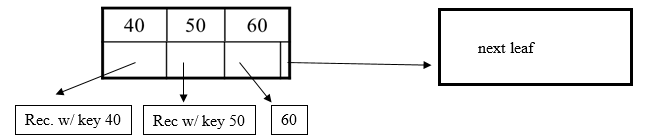
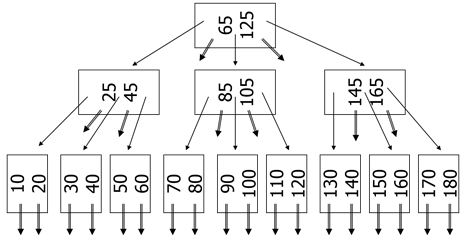
Example with $d$=2:
How large should we make d?
Example:
Key size = 4 bytes
Pointer size = 8 bytes
Block size = 4096 byes
$2d \times 4 + (2d+1) \times 8 \le 4096$
$d = 170$
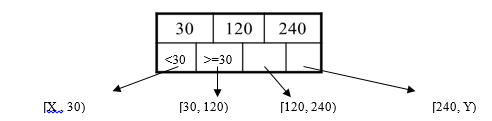
Searching a B+ Tree
Exact key values: Select name From people where age = 25
Start at the root
Proceed down, to the leaf
Range Queries: Select name From people where age > 25 or age <10
Start at root
Proceed down to leaf
Then sequential traversal (B+ > B-Trees)
In Practice
Typical order: 100. Typical fill-factor: 67%.
average fanout = 133
Typical capacities:
Height 4: 1334 = 312,900,700 records
Height 3: 1333 = 2,352,637 records
Can often hold top levels in buffer pool:
Level 1 = 1 page = 8 Kbytes
Level 2 = 133 pages = 1 Mbyte Level 3 = 17,689 pages = 133 MBytes
Insertions on a B+ Tree
Insert (K, P)
Find leaf where K belongs, insert
If no overflow (2d keys or less), halt
If overflow (2d+1 keys), split node, insert in parent:
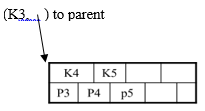
Internal node example:

If leaf, keep K3 too in right node. When root splits, new root has 1 key only. (That’s why root is special for degree satisfaction)
Example:
Insert 19:
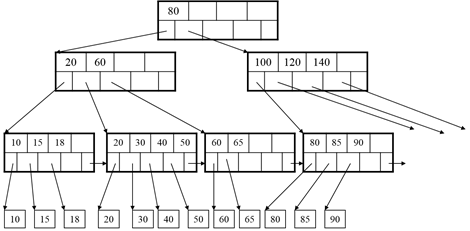
After Insertion:
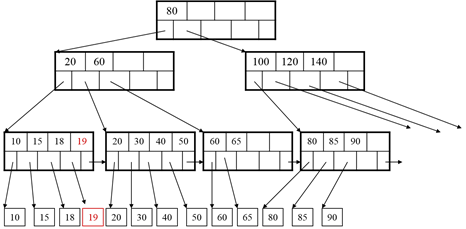
Insert 25:
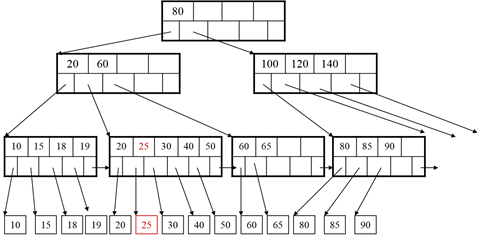
Need to split:
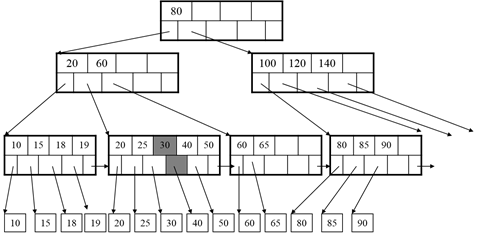
After the split:
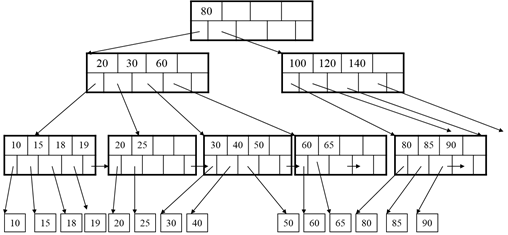
Delete 30:
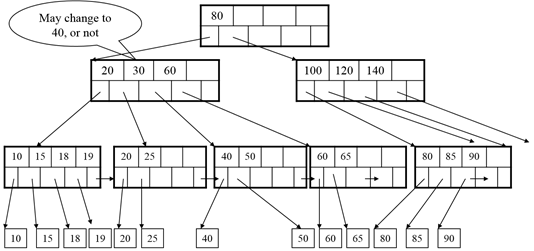
Delete 25:
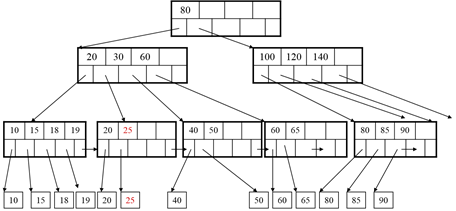
After deleting 25 – we need to rebalance
Number of keys < d
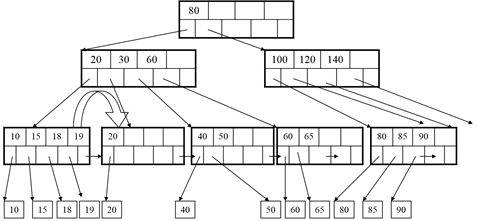
Now let’s delete 40:
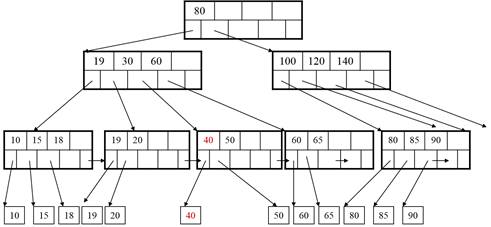
After deleting 40 a rotation is not possible
We need to merge
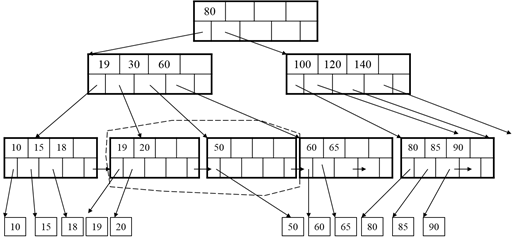
Finally: