What happens when the data gets really really big?
Computers have physical limitations
- RAM
- Processors
- Disk
RAM is getting cheaper, processors more cored, disk is getting bigger and cheaper.
But data is winning the race.
We can put data on supercomputers with millions of cores and exabytes or RAM and disk. But the price of a supercomputer is much more than the price of the same # cores, memory and disk space bought at best buy.
We call supercomputers – supercomputing
We call supercomputing on best-buy hardware “big-data”
Blue Waters supercomputer cost 208 million dollars. It can sustain 1 PetaFLOP per second.
AMD Ryzen processor with 1=484GigaFLOPS for $200
How many AMD computers will it take to have the same FLOPS-power as Blue Waters? How much will it cost?
1 PetaFLOPS = 1,000,000,GigaFLOPS / 484 = 2,066 computers
=$413,000
So, the question is: how do we turn 2,000 best buy computers into a supercomputer?
When data gets really really big we can’t fit it on a single HDD. Or if we could, the processors couldn’t compute it.
BTW — an AMD graphics card hits 75TFLOPS for $2,000 (1000/75 = 14 * 2000 = $28,000 for one PFLOP)
PS5 can do about 10TFLOPS for $400 (1000/10) = 100 PS5s
History
Data warehousing, OLAP, OLTP -> Streaming -> big data
Only store important things columns -> sample rows -> keep everything
HDFS

Hadoop file system – Started at Google and Yahoo. Yahoo released a paper.
Hadoop
Hadoop was started based on Yahoo’s paper by Michael Cafarella (Nutch) and Doug Cutting (Lucene) – named after Doug’s son’s toy elephant
Hadoop includes MapReduce and HDFS
- MapReduce is the computation
- Job Tracker
- TaskTracker
- HDFS is a filesystem just like ext3 or NTFS. But it’s a distributed filesystem that can store exabytes of data on best buy machines.
- Namenode
- Datanode
Each machine has one or more of these.
We will focus on HDFS and databases that run on HDFS.
As you add more machines you increase capability linearly (almost)
JobTracker
Accepts jobs, splits into tasks, monitors tasks (schedules, reschedules)
NameNode
Splits a file into blocks, replicates.
>sudo su
>hdfs namenode
Data never flows through the namenode, the name node just points to where the data blocks exist.
>hdfs dfs -ls /-cat... >hdfs datanode
Say we have 3 Hadoop Servers with 2 tuples, block size is 8 bytes, split on ‘ ‘.
(A, we like toast) (B, toast is like bread)
Where is A stored? Perhaps its split onto different disks via HDFS. Same with B.
Server1 Server2 Server3 (A, We like) (B, toast is) (A, toast) (B, bread) (B, like)
Say we have 4 Hadoop Servers with 4 documents, block size is 15 bytes, split on ‘ ‘.
(A, what though the odds be great or small) (B, old Notre Dame will win over all) (C, while Her loyal sons and daughters) (D, march on to victory)
Where is A stored? Perhaps its split onto different disks via HDFS. Same with B.
Properties of HDFS
Reliable – data is held on multiple data nodes (replicated =2 or 3), and if a data node crashes the namenode reshuffles things.
Server1 Server2 Server3
(A, We like) (B, toast is) (A, toast)
(B, bread) (B, like)
(B, toast is) (A, We like) (B, bread)
(A, toast) (B, like)
Green nodes are replicas
Scalable – can scale code from 1 machine to 100 machines to 10000 machines – with the same code.
Simple – APIs are really simple
Powerful – can process huge data efficiently
Other projects that we will talk about
Pig – a high level language that translates data processing into a Mapreduce job. Like Java gets compiled into byte code. Half of jobs at Yahoo are run with Pig
Hive – Define SQL that gets translated to MapReduce jobs. About 90% of Facebook queries use Hive.
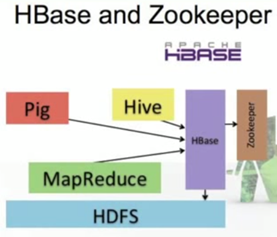
But these are all batch processes – they take a long time to fire up and execute.
HBase – provides simple API to HDFS that allows incremental, real time data access
Can be accessed by Pig, Hive, MapReduce
Stores its information in HDFS – so data can scale and is replicated, etc.
Hbase is used in Facebook Messages – each message is an object in an HBase table.
Zookeeper – provides coordination and stores some Hbase meta data.
Mahout (ML), Ganglia (monitor), Sqoop (talk to MySQL), Oozie (workflow management – like cron), flume (streaming loading into hdfs), Protobuf (google) – Avro – Thrift (serialization tools)
HDFS
Supports read, write, rename and append. It does not support random write operations.
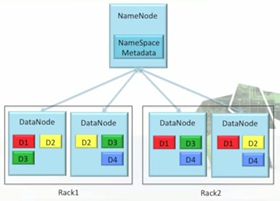
Optimized for streaming reads/writes of large files. Bandwidth scales linearly with nodes and disks.
Built in redundancy – like we talked about before.
Auto addition and removal – one person can support an entire data center.
Usually one namenode, many datanodes on a single rack. Files are split into blocks. Replicated to 3 (typically); replication can be set on a file by file basis.
Namenode manages directories, maps files to blocks. Checkpoints periodically.
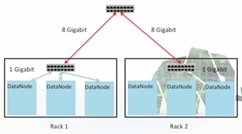
Supports Large clusters
Typically:
- 40 nodes to a rack
- Lots of racks to a cluster
- 1Gigabit/s between nodes
- 8-100 Gb/s between racks (higher level switch)
Rack aware
Files are written first to the local disk where the writer exists (MapReduce) and then to rack-local disks.
Replica monitoring makes sure that disk failures or corruptions are fixed immediately by replicating the replicas.
Typically 12TB can be recovered (re-replicated) in 3-5 minutes.
Thus, failed disk need to be replaced immediately as needed in RAID systems. Failed nodes not needed to be replaced immediately.
Failure
Happens frequently – get used to it. (best buy hardware)
If you have 3K nodes, with 3 year amortized lifespan… how many nodes die per day?
- 3*365 = approx. 1000.
- 3000/1000 means 3 nodes will die per day on average (weekends, fall break, etc).
“Data centric computing”
Past 50 years, data moves to computation… now computation moves to the data. (HDFS mapreduce enables this)