Hashtable Indexes

Secondary storage hash tables are much like main memory ones

Recall basics:
                There are  buckets
                A hash function f(k) maps a key k to {0, 1, …, n-1}
                Store in bucket f(k) a pointer to record with key k

Secondary storage: bucket = block, use overflow blocks when needed

Assume 1 bucket (block) stores 2 keys + pointers

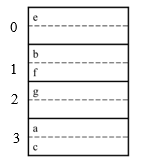
h(e)=0
h(b)=h(f)=1
h(g)=2
h(a)=h(c)=3

Search for a:
Compute h(a)=3
Read bucket 3
1 disk access

Insertion:

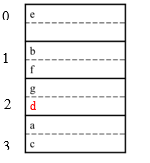
place in right bucket, if space
E.g. h(d)=2

Overflow blocks

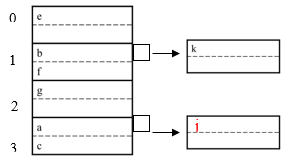
Create overflow block, if no space
E.g. h(k)=1

Performance

Excellent, if no overflow blocks

Degrades considerably when number of keys exceeds the number of buckets (I.e. many overflow blocks).

Extensible Hash Table:

Allows hash table to grow, to avoid performance degradation
Assume a hash function h that returns numbers in {0,…,2^k – 1}
Start with = 2^i≪2^k , only look at first i most significant bits 𝑖=1, 𝑛=2^𝑖, 𝑘=4 bit int (or whatever)

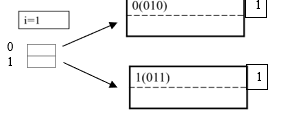
Note – we only look at the first bit.

Insert 1010

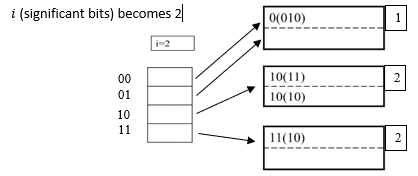
Need to extend table, split blocks:

Noww insert 0000,
then 0101

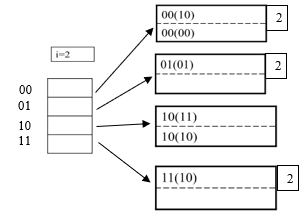
What if we
inserted 0001?
This would
“extend” the hashtable again i=3

Extensible Hash Tables performance
No overflow blocks: access always one read
BUT:
Extensions can be costly and disruptive (Power of 2)