Relational Algebra
Basic:
$R$ $\sigma_{C}(R)$
$\Pi_{(a_1\ldots,a_k )}(R)$
$R_1\times R_2$
$R_1\cup R_2$
$R_1-R_2$
$\rho_{S(a_1,\ldots,a_n )}(R)$
Derived:
$R_1\bowtie R_2$
$R_1 \bowtie_\theta R_2$
$R_1\cap R_2$
Additional:
$\gamma_{(a,f(b))}(R)$
$\delta(R)$
Building Complex Expressions
Algebras allow us to express sequences of operations in a natural way.
Example:
- in arithmetic algebra: (x + 4)*(y – 3)
- in stack “algebra”: T.push(S.pop())
Relational algebra allows the same.
Three notations, just as in arithmetic:
- Sequences of assignment statements.
- Expressions with several operators.
- Expression trees.
Sequences of Assignments
Create temporary relation names. Renaming can be implied by giving relations a list of attributes.
Example: $R_3 = R_1 \bowtie_\theta R_2$ can be written:
$R_4=R_1\times R_2$
$R_3 =\sigma_\theta (R_4)$
Find Salespersons who have a commission less than or equal to 11 and are managed by manager with id of 44.
$R=\sigma_{(\textrm{“comm”}<11\wedge\textrm{“manager\_id”}=44)} (\textrm{Salesperson})$
Find Names of Customers who bought an item on February 12th.
$R = \textrm{Sale}\bowtie\textrm{Customer}$
$S= \sigma_{(\textrm{date=02/12})} (R)$
$T =\Pi_{(\textrm{cust\_name})} (S)$
Expressions with several operators
Example: the theta-join $R_3 = R_1 \bowtie_\theta R_2$ can be written $R_3 =\sigma_\theta (R_1\times R_2)$
Precedence of relational operators:
- Unary operators — select, project, rename — have highest precedence, bind first.
- Then come products and joins.
- Then intersection.
- Finally, union and set difference bind last.
But you can always insert parentheses to force the order you desire.
Find Products made in Peru
$R=\Pi_{(\textrm{prod\_desc})} (\textrm{Product}\bowtie(\sigma_{(\textrm{country=’Peru’})} \textrm{Manufacturer}))$
Expression Trees
- Leaves are operands — either variables standing for relations or particular, constant relations.
- Interior nodes are operators, applied to their child or children.
Find Salespersons who sold something to Customers with less than 50000 in the bank.
$\Pi_{(\textrm{salpers\_name})} (\textrm{Salesperson}\bowtie(\textrm{Sale}\bowtie\sigma_{(\textrm{curbal}<50000)} \textrm{Customers}))$
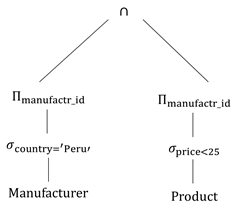
Example: Find all manufacturer ids that sell a product for less than $25 made in Peru.
Find Customers or Salespersons who live in Tokyo
$\rho_{\textrm{name}} (\Pi_{\textrm{cust\_name}} (\sigma_{(\textrm{city =’Tokyo’})}(\textrm{Customer}))) \cup \rho_\textrm{name} (\Pi_{\textrm{salpers\_name}} (\sigma_{(\textrm{office=’Tokyo’})}(\textrm{Salesperson})))$
Operations on Bags
(and why we care)
Relational Algebra uses set-semantics, which is why $\Pi$ eliminates duplicate tuples.
Databases actually use bag-semantics:
Union: $\{a,b,b,c\}\cup\{a,b,b,b,e,f,f\} = \{a,a,b,b,b,b,b,c,e,f,f\}$
(add the number of occurrences)
Difference: $\{a,b,b,b,c,c\}-\{b,c,c,c,d\} = \{a,b,b\}$
(subtract the number of occurrences)
Intersection: $\{a,b,b,b,c,c\}\cap\{b,b,c,c,c,c,d\} = \{b,b,c,c\}$
(minimum of the two numbers of occurrences)
Selection: preserve the number of occurrences
Projection: preserve the number of occurrences (no duplicate elimination in real databases)
Cartesian product, join: no duplicate elimination
Summary of Relational Algebra
Why bother? Can write any RA expression directly in C++/Java, seems easy.
Two reasons:
- Each operator admits sophisticated implementations (think of $\bowtie$,$\sigma_theta$)
- Expressions in relational algebra can be rewritten: optimized