(Some of this content from Nathan Bastian)
Remember Linear Regression
Linear regression is a simple approach to supervised learning. It assumes as it assumes $Y$ is dependent on $X_1, X_2, \ldots X_p$ and that this dependency is linear.
Most modern machine learning is basically fancier versions of linear regression where the goal is: predict $Y$ from $X$ by $f(X)$, where $f$ is a fancy neural network or something.
Linear Regression model
- Input vector: $X^T = (X_1, X_2, \ldots X_p)$
- Output $Y$ is real-valued (quantitative response) and ordered
- We want to predict $Y$ from $X$, but before we actually do the prediction, we have to train the function $f(X)$.
- At the end of training, we have a function $f(X)$ to map every $X$ into an estimated $Y$ (we call $\hat{Y}$).
What does $f(X)$ look like as a linear regression model?
$$f(X)=\beta_0+\sum_{j=1}^{p} X_j\beta_j$$
$\beta_0$ is the intercept and $\beta_j$ is the slope for the $j$th variable $X_j$, which is the average increase in $Y$ when $X_j$ is increased by one unit and all other $X$’s are held constant.
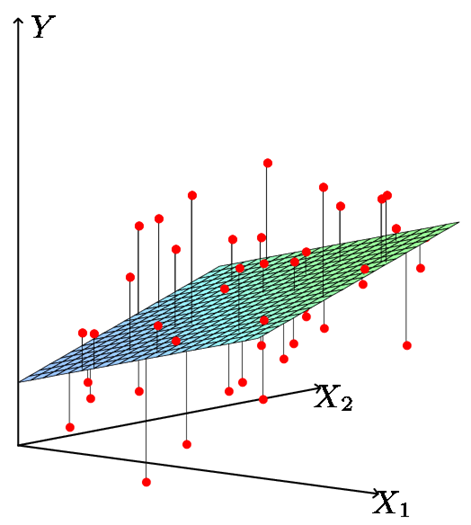
The job of OLS is to calculate this hyperplane
Hypothesis Testing
$H_0$: all slopes equal 0 ($\beta_1=\beta_2=\ldots=\beta_p=0$).
$H_a$: at least one slope $\ne$ 0.
We use the ANOVA table to get the F-statistic and its corresponding p-value. If p-value < 0.05, reject $H_0$. Otherwise, all of the slopes equal 0 and none of the predictors are useful in predicting the response.